12. Jozef VIVODA :"Analysis of stability of 2TL SI non-extrapolating predictor/corrector scheme in the limit of infinite time step"

1. Introduction

Linearized version of Euler Equations system (EE) is analysed in the limit of infinite time step. Two time level semi-implicit non-extrapolating predictor/corrector (2TLSI-NES PC) time marching scheme is applied on linearized space continuous EE. Results are independent of model space discretisation and their validity can be generalized for other models as well.

EE system is formulated using s hydrostatic pressure based coordinate . Prognostic variables are divergence (D), temperature (T ), logarithm of surface pressure , vertical divergence d3 and rescaled pressure departure :

2. Linearized model

Analyses of stability is analytically tractable, if analysed system is linear only. Therefore, the nonlinear EE has to be linearized around atmospheric background state. Background state was chosen to be in rest, hydrostatically balanced, over flat terrain (it could be understood as horizontally independent), isothermal. There are only two degrees of freedom remaining in such a choice of background state , background-state temperature and background-state surface pressure.

Atmospheric state described by prognostic variables can be expressed as infinitesimal perturbation around background state (denoted by a bar) :

Before the analysis, the integral operators that appear in the system are replaced by derivative operator . The logarithm of surface pressure will disappear from the equations. Classical linearization yields then to the following linear system (M) :

The parameter α is equal to 1 for the purpose of following analyses. If model was formulated using , then α would be the ratio of T * to the background-state temperature. This possibility will be discussed in the summary.

3. Two time level semi-implicit non-extrapolating predictor/corrector scheme (2TLSI-NES)

The scheme is called non-extrapolating since unknown state at time t + Δ t /2, appearing in two time level scheme formulation, is approximated using relation

In the following, time instant t + Δ t /2 is excluded from equations and relation (3) is used implicitly everywhere.

If linearized equations system (2) is referred as M, semi-implicit linear model as L, the nonlinear residual as R and model state vector X, then the predictor of 2TLSI-NES yields :

Semi-implicit linear model can be obtained from M just by setting the background-state values of T and πs to T* and πs* respectively. Here T* is the reference temperature of semi-implicit linear model and πs * is analogically the reference surface pressure.

Non-extrapolating predictor allows to compute first guess at time t + Δ t , using just state at time instant t . This approach is only first order accurate. This is not an obstacle when predictor/corrector scheme is used since second order accuracy is restored during corrector steps. The k-th corrector step is formulated :

Parameter ε is first order decentering factor.

4. Analyses of stability

We examine the stability of the normal modes of the time-continuous system. Following Bénard et al. (2002) the geometric structure of the normal modes is :

Notation H represents the height of the isothermal atmosphere with temperature T* . Notation n corresponds to n=i +1/(2H) with being the vertical wavenumber. Notation k is used for horizontal wavenumber.

Classical Von Neumann stability analysis is used with amplification rate of the scheme λ defined as :

for predictor and

for k-th corrector step.

Centred non-extrapolating scheme and also non-extrapolating scheme with first order decentering are truly two time level schemes. Their contains only physical modes and no computational. Therefore four solutions of λ exist in EE system, two represent gravity modes and two represent acoustic modes.
The fact that reference and background-state temperatures are chosen to be isothermal leads to possibility to use linear relation between them :

Analyses with first order decentering : Predictor

First analyses of predictor is carried out. Relations (6), (7) and (9) are substituted into (4). Structure equation is found as a determinant of model state transition matrix. Solving structure equation for λ four solutions are found.

All solutions are real. First two modes λ 1(0) and λ 2(0) are stable for ε ³  0. Analysing other two modes the condition for predictor to be stable is found :

If the predictor is not decentered ( ε =  0) then it is unconditionally unstable. Condition could be written as a condition for the range of actual temperature dependent on current value of T*.

Analyses with first order decentering : Corrector

Substituting (6), (7), (9) and (10) into (5), we obtain forth order polynomial equation of every mode of predictor (CAUTION, this approach has been found to be methodologically wrong. Results for predictor are correct but results for corrector presented here are wrong. More details about the methodology can be found in the appendix). Subsequently the solutions of amplification rate are found for k-th corrector :

There are recurrence relations for the third and the forth mode. Notation λn (k-1) means any of the mode from previous corrector (or predictor in the case of the first corrector). If any of first two stable modes (λ1(k-1) or λ2 (k-1)) enter recurrence relations then the following modes are stable.

Before analyses of mixed modes the analyses of "clean" modes is done. If we consider that :

we could then write for the amplification factor of the third "clean" mode of k-th corrector :

This mode is stable in the limit of infinity iterations, if the condition -1 £ a £ 1 is satisfied.

If :

is considered, then amplification rate of the forth "clean" mode of k-th corrector is :

This mode is stable in the limit of infinity iterations, if the condition -1/2 <=a <= infini is satisfied.

There are other mixed modes. Their analytical analyses is practically impossible due to oscillating character of the third mode. Their behaviour was studied experimentally and it was found that for the first corrector those modes are the most unstable one. The behaviour of these mode is still in the phase of experimental research.

There is plotted absolute value of the most unstable mode on figure 1 for predictor and first five correctors for the first order decentering factor ε = 0.1 .

It is interesting to point that the effect of first order decentering is simply the shift of the curves down along the y-axis by the factor .

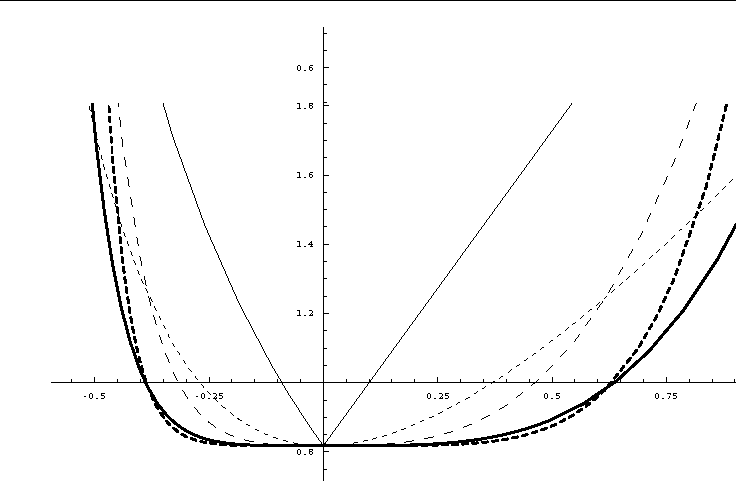
fod-lambda-limit.gif

Figure 1: The absolute value of the growth rate of the most unstable mode of the non-extrapolating two-time-level semi-implicit predictor/corrector scheme. The s vertical coordinate is used and the first order decentering factor is ε = 0.1. Predictor, corrector first, second, third and forth are plotted using thin solid line, thin short dashed line, thin long dashed line, thick solid line and thick short dashed line.

5. Summary

We analysed the two time level semi-implicit non-extrapolating predictor/corrector scheme applied to the space continuous Euler equations. We found that to achieve stability of the first or second corrector it is necessary to apply decentering. We studied first order decentering. It was found that if the stability shall be achieved for large range of temperatures the value of first order decentering factor has to be very large and the accuracy of the scheme is decreased. To get over this problem the second order decentering shall be applied.

We found that for the "clean" modes scheme converge for the range of temperatures :

This results anyway can not be generalized yet since there exist mixed modes we could not analytically analysed. This research is still in progress.

It is important to noticed that we analysed also system formulated with pseudo-vertical divergence. It was found that the system is extremely unstable and it diverge.

6. Last minute : Methodology of stability analyses of predictor/corrector schemes

The analyses of stability of predictor/corrector scheme seems to be at a first glance methodologically the same as the analyses of SI scheme. This is true only partially and it is very easy to obtained wrong results doing wrong assumption.

We assume, for the purpose of this appendix, that the 2TL-NES scheme with one corrector can be written for linearized system as :

Here MSI is the matrix appearing from the fact that semi-implicit approach is used. And M P, MCI and MC2 are matrices which represent RHS of predictor resp. corrector step.

There exists two methodological approaches how to compute the growth rate :

1. "matrix" method. Using this method one has to invert MSI and to calculate the total amplification matrix of the PC scheme. This yields :

Then the growth rate of particular mode is found as the eigenvalue of the matrix MPC.

2. "polynomial" method. We assume that amplification rates for predictor and corrector are :

and we substitute those assumptions into (17). Eliminating variables the set of two polynomial equations for two variables λ * and λ (t-Dt) is obtained. The roots of those set then represent the growth rate of the scheme.

When SI scheme is considered those two approaches are equivalent.

When analysing PC scheme the "polynomial" method is wrong, because we assumed , which is not valid any more. It would be valid only in the case when X(t), was an eigenvector of MP and also MCI. This assumption is not satisfied in our system and therefore the results by using "polynomial" approach are wrong.

The matrix method is only correct one for the predictor/corrector analyses of stability.



The previous ALATNET PhD and Post-Doc Studies Home Newsletter 21 & 4