arpege

5.2 Les variables mises à jour

Une fois les paramètres ci-dessus initialisés par la lecture du fichier, on effectue une mise à jour de certains d'entre eux ( sur la base de données mensuelles en particulier ).
Sur mer et sur banquise, on modifie en outre ( suivant la position de la banquise ):
- l'indice terre-mer ( 1 sur banquise, 0 sur mer ).
- la longueur de rugosité: 0.001 sur la banquise.
- l'albédo de surface ( 0.65 sur glace, 0.07 sur mer ); la valeur sur glace peut être augmentée en cas de neige.

5.3 La thermodynamique

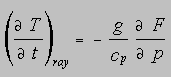
Comme dans le modèle EMERAUDE, on tient compte de la variation de C_p et de R avec q ( humidité spécifique de la vapeur d'eau ) dans le cas de l'air humide, soit

R = R_a + ( R_v - R_a ) q

C_p = C_{p_a} + ( C_{p_v} - C_{p_a} ) q

De plus, dans ARPEGE, on prend maintenant en compte la variation des chaleurs latentes de vaporisation et de sublimation avec la température soit

L_v ( T ) = L_v ( T^* ) + ( C_{p_v} - C_l )( T - T^* )

L_s ( T ) = L_s ( T^* ) + ( C_{p_v} - C_i )( T - T^* )

T^* étant la température du point triple, T^* = 273.16 K

La chaleur latente de fusion L_f ( T ) est alors égale à L_s ( T ) - L_v ( T )

Ce détail a en fait peu d'influence sur les résultats de la prévision à courte et moyenne échéance et pourrait apparaître comme un raffinement inutile. Cependant, cette dépendance permet d'obtenir une description exacte de tous les cycles énergétiques dans l'atmosphère, point qui peut se révéler fondamental dans le cas d'une simulation climatique.

5.4 Les paramétrisations

Quelques généralités

Le but de la partie physique du modèle consiste à fournir un forçage correct à la dynamique et à donner des évaluations réalistes des flux qui définissent le temps sensible : précipitations, rayonnement... La partie physique calcule donc les différents échanges énergétiques entre l'atmosphère et les sources externes. Ces sources sont, pour l'atmosphère global, le soleil, les océans et dans une moindre mesure les continents. Les processus d'échange d'énergie sous ces différentes formes entre ces sources externes et l'atmosphère sont extrêmement variés et hautement interactifs donc très complexes.

Chaque paramétrisation physique peut être considérée comme une boîte noire dans laquelle on introduit les variables à grande échelle et qui doit fournir en sortie les variations temporelles de ces variables dues aux phénomènes physiques, phénomènes irréversibles et/ou se produisant à une échelle inférieure à celle de la maille. Ces boîtes contiennent donc des équations traduisant au mieux la réalité. L'ajustement de ces équations est tributaire naturellement de la partie dynamique ( taille de la maille notamment ) mais aussi et surtout du temps de calcul disponible. Tout le problème consiste donc à allier au mieux les impératifs opérationnels et le meilleur réalisme.

5.4.1 Le rayonnement

Quelques généralités :

Le soleil est la source d'énergie primaire de la machine thermique. Il rayonne comme un corps noir dont la température de surface serait 6000° K. Il émet dans les longueurs d'onde allant de 0.25 à 5 µm. Le rayonnement solaire est absorbé dans l'atmosphère en raison de la présence de corps absorbants: l'oxygène, l'azote et surtout l'ozone dans le domaine de l'ultra-violet, la vapeur d'eau et, à un degré moindre, le gaz carbonique dans le domaine de l'infra-rouge.
Le rayonnement solaire subit également une diffusion qui disperse dans toutes les directions les rayons incidents. Elle est due aux molécules d'air atmosphérique, aux aérosols et aux masses nuageuses.
La surface terrestre absorbe une partie du rayonnement incident et en réfléchit l'autre partie ( albédo de surface ).
La terre rayonne également, cette émission dépend de la température et de l'émissivité de la surface. Ce rayonnement est presque totalement absorbé par l'atmosphère.
Les couches atmosphériques émettent aussi un rayonnement égal à celui qu'elles absorbent ( loi de Kirchoff ).

On le constate, les phénomèmes mis en jeu sont complexes et les paramètres à calculer très nombreux. Ceci explique pourquoi le rayonnement est l'une des paramétrisations les difficiles à réaliser.

Le but de cette paramétrisation est de calculer les différents flux radiatifs au sommet et à la base de chaque couche atmosphérique considérée, pour en déduire une tendance de température due au rayonnement. Cette tendance est proportionnelle à la divergence de ces flux ( comptés positivement vers le bas ) soit:

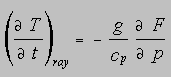
Un flux radiatif s'exprime comme une puissance par unité de surface ( W.m¯² ).

Dans le schéma utilisé dans ARPEGE, la rapidité de calcul a été privilégiée aux dépens de l'exactitude absolue, l'argument étant qu'il est plus important de tenir compte des interactions à très court terme avec la température de surface du sol continental ou avec les fluctuations de la nébulosité, que de contrôler les biais dus à la configuration spectroscopique très particulière d'une certaine bande d'absorption ( cf intégration spectrale ).

L'équation fondamentale de cette paramétrisation est l'équation du transfert radiatif. Cette équation exprime comment varie la luminance énergétique L ( intensité reçue dans une direction donnée ) lorsqu'une épaisseur d'un milieu est traversée par un rayon.

La luminance évolue lors de la traversée par 3 effets :
- l'extinction : perte de rayonnement par diffusion et absorption. Elle est proportionnelle à la luminance et à la masse de matière traversée.
- gain par diffusion : apport dû aux rayons diffusés dans la direction incidente.
- l'effet source tel le rayonnement du corps noir, qui dépend de la température.

L'intégration de cette équation, écrite en différentielle par rapport à l'épaisseur optique et pour les flux diffus, doit se faire:
- sur le domaine angulaire ( solide ) c'est-à-dire par rapport à tous les angles d'incidence des rayons diffus entrant,
- sur le domaine vertical c'est-à-dire sur une couche infiniment fine aux propriétés optiques supposées homogènes,
- sur toutes les longueurs d'onde du spectre,
- sur toutes les épaisseurs optiques de l'absorbant c'est-à-dire par rapport aux chemins optiques des rayons.
et ceci pour chacun des absorbants !

Cette quadruple intégration entraîne des calculs gigantesques mais théoriquement possibles, on est donc amené à faire un certain nombre d'hypothèses simplificatrices. On ne donne par la suite que certaines de ces hypothèses ; pour une approche plus complète de cette paramétrisation très compliquée, on se reportera à :
- La paramétrisation du rayonnement ( conférence de J.F. GELEYN, rédigé par Y. ERNIE )
- et à l'article de B. RITTER, J.F GELEYN. Février 1992. A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate situations. Monthly Weather Review ( volume 120, N° 2 ).

5.4.1.1 Intégration angulaire

5.4.1.1.1 facteur de diffusivité d'une couche

Ayant supposé, l'axisymétrie verticale on définit un facteur de diffusivité pour traduire l'absorption par une épaisseur de la couche traversée.
Pour un rayonnement déjà diffus arrivant de toutes les directions et rencontrant une certaine épaisseur optique d'absorbant, les rayons verticaux rencontrent moins de matière que les rayons obliques et ont donc à la sortie une intensité plus grande. On suppose pour simplifier que le rayonnement rentre et sort isotrope et que l'effet de la couche se résume à un facteur de diffusivité que l'on définit à partir du rapport du flux sortant au flux entrant. Le principe est de représenter la transmission de tous les rayons à travers la couche par un seul rayon de direction théta déterminée empiriquement.

5.4.1.1.2 l'approximation des deux flux ( "two-stream" ).

On suppose que l'isotropie permet de décrire le champ de rayonnement diffus uniquement à l'aide du flux descendant et du flux montant. On définit le flux net comme la différence entre le flux descendant ( compté positivement ) et le flux montant.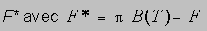
A ces deux flux on ajoute le flux correspondant au rayonnement solaire parallèle.

On écrit le système d'équations pour le rayonnement solaire visible ( 3 équations ) liant les flux diffus vers le haut, diffus vers le bas F et solaire parallèle S ( vers le bas ).
Pour le rayonnement thermique, le système s'écrit sous la même forme, à condition de remplacer les flux par les flux modifiés :

et d'abandonner les termes faisant intervenir le flux solaire.

5.4.1.2 Intégration verticale

Il s'agit là d'une intégration sur une couche aux propriétés homogènes.
On intègre le système "two stream" pour une couche supposée homogène ( coefficients constants ) et on obtient un système linéaire de 3 équations qui lient les flux entrant aux flux sortant. Si on suppose que l'on connait les coefficients pour les n couches du modèle, on obtient n systèmes de 3 équations pour calculer 3( n+1 ) flux. Pour fermer le système on a besoin des conditions aux limites.

On suppose aussi que les flux sortant d'une couche entrent dans la couche adjacente.

Pour la partie thermique, on doit intégrer sur la couche les termes :

Il faut faire une hypothèse sur la variation de la fonction de Planck dans la couche. On suppose simplement que B( T ) est constant dans la couche ( couche isotherme ) avec une discontinuité à la frontière.

Le traitement des nuages

Les calculs précédents sont faits par ciel clair. Le fait de rajouter les nuages revient à utiliser des coefficients ( dans les systèmes d'équations ) pour la partie de ciel clair et d'autres pour la partie nuageuse. Il y a donc pour chaque couche, non pas 3 mais 6 équations, les deux effets étant pondérés par la nébulosité.
On fait les hypothèses suivantes :
- chaque nuage s'étend verticalement sur toute la couche et la nébulosité est constante pour toute la couche,
- il n'y a pas d'effet latéral entre nuage et ciel clair.

Sur l'interface horizontale, deux solutions classiques sont alors possibles :
- le recouvrement aléatoire : aucune hypothèse n'est faite concernant les nébulosités des couches adjacentes. Les coefficients des matrices sont calculés comme les sommes de deux types de coefficients, les uns intégrant les contributions des nuages aux épaisseurs optiques, les autres non. Les coefficients pondérateurs étant logiquement, les nébulosités partielles et leurs compléments à 1.

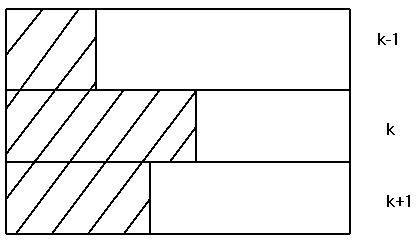
- le recouvrement maximal : les fractions nuageuses de couches adjacentes présentent un recouvrement maximal. Il faut alors considérer en détail les flux aux interfaces. Les flux sont calculés comme étant la somme de flux "partiels" clairs et nuageux. On est amené à considérer deux types de systèmes : le premier n'intégrant pas les effets des nuages, produit des flux "partiels clair", le second intégrant ces effets, produit des flux "partiels nuageux". La résolution de ces deux types de systèmes doit se faire en parallèle puisqu'en fonction de la configuration nuageuse, les flux "partiels" interagissent.

La deuxième méthode est meilleure mais plus compliquée donc plus coûteuse. En pratique ( au niveau des résultats du modèle ), les deux méthodes donnent des résultats similaires, à condition de mettre moins de nébulosité dans la première méthode que dans la seconde, ce qui se fait en définissant des humidités critiques différentes.
Dans le code, les deux options, celle plus physique du recouvrement maximum des nuages adjacents et celle du recouvrement au hasard des parties nuageuses séparées par des couches d'air clair, sont disponibles. Actuellement l'option du positionnement des nuages au hasard les uns par rapport aux autres suivant la verticale est choisie, il ne s'agit ici que d'un problème de coût de calcul.

Pour déterminer la nébulosité, on diagnostique le contenu liquide nuageux ( humidité spécifique liquide ou glace ). On calcule pour chaque couche la partie condensée q_cond, il s'agit de l'eau maximale extractible lors des mouvements verticaux dans le nuage ( le long d'une adiabatique saturée ), compte tenu des caractéristiques locales ( T et p ).

On part de

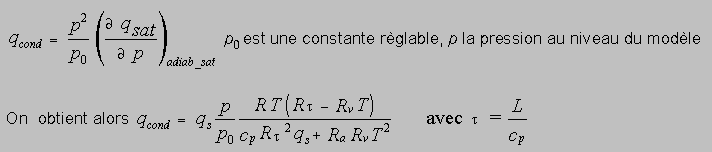
On cherche ensuite la partition eau/glace. Pour ce faire, on introduit une fonction f de la température donnant la proportion de glace dans une particule nuageuse. Dans ARPEGE, on modélise cette fonction en postulant que la proportion de glace est liée à l'intégrale de l'écart entre tension de vapeur saturante par rapport à l'eau liquide et tension de vapeur saturante par rapport à la glace. Après un ajustement à l'aide d'une gaussienne, on obtient :

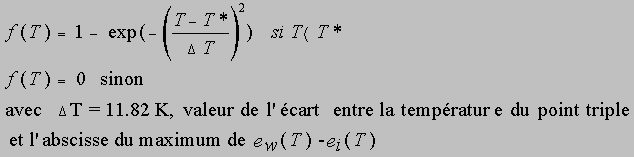
La valeur de f( T ) étant connue, la partition eau/glace est calculée par:
q_l = ( 1 - f( T ) )q_cond et q_i = f( T )q_cond

Ceci permet de distinguer les phases liquide et solide, chacune d'elles ayant des propriétés optiques différentes ( coefficient d'absorption ).

Remarque :

Pour corriger le déficit radiatif global constaté au sommet de l'atmosphère, on réduit la réflectivité des nuages en majorant leur contenu en eau condensée ( liquide et solide ).

Calcul de la nébulosité convective à un niveau donné.

La nébulosité en nuages convectifs est calculée au pas de temps précédent après les calculs complets concernant la convection, trois informations sont alors stockées : les indices de base et de sommet de couches pour ce type de nébulosité et la nébulosité totale.

Cette dernière est calculée d'après Tiedtkte ( 1988 ) par Nc_tot = min ( 0.5 , p.Rc_surf )
avec Rc_surf : taux de pr´cipitations convectives au sol et p pente fixe égale à 3000.

Au pas de temps où elle est utilisée, Nc_tot est convertie en une nébulosité locale à tous les niveaux compris entre la base ( Ic_b ) et le sommet ( Ic_t ) de la couche de nuages convectifs. Cette conversion prend en compte l'utilisation possible dans le schéma de rayonnement, des deux types de recouvrement :

- s'il s'agit du recouvrement maximal, Nc = Nc_tot .
- s'il s'agit du recouvrement aléatoire, Nc = 1 - ( 1 - Nc_tot ) ( 1 / ( Ic_b - Ic_t + 1 ) ) .

Calcul de la nébulosité stratiforme à un niveau donné.

Le calcul de la nébulosité stratiforme Ns utilise exactement l'algorithme décrit par Geleyn ( 1980 ) soit

Ns = max² ( 0 , ( q - Hu_c.q_sat ) / ( q_sat - Hu_c.q_sat ) )

La nébulosité ainsi calculée dépendra d'une humidité critique Hu_c, seuil qui est fonction de la verticale. Ce seuil d'humidité est paramétré par la fonction polynomiale suivante :

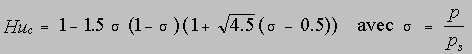
En outre Ns est nulle pour tous les niveaux où l'énergie statique sèche est inférieure à l'énergie statique sèche de surface ( pas de nuages : couche bien mélangée ).

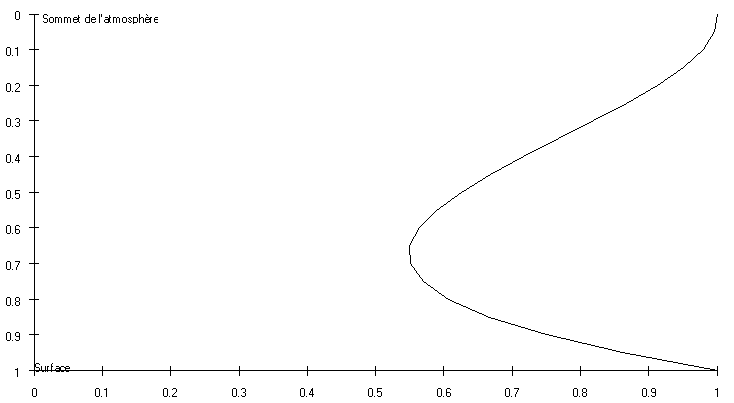
Remarque importante :

Il n'y a pas actuellement de nébulosité associée à la convection peu profonde, ceci constitue probablement l'une des plus importantes faiblesses de ce schéma de diagnostic nuageux, qui a pourtant l'air bien calibré.

La nébulosité totale est ensuite obtenue en utilisant la combinaison classique suivante :

Nt = 1-( 1-Ns )( 1-Nc ).

5.4.1.3 Intégration spectrale

On distingue deux calculs différents suivant que l'on considère les gaz et les corps gris.

En effet les variations des coefficients d'absorption spectraux des gaz en fonction de la longueur d'onde sont telles, que l'on doit, pour réaliser une intégration spectrale, utiliser une formulation non linéaire vis à vis des quantités de gaz traversé.

Cas des gaz :
Pour l'absorption les caractéristiques des différents gaz actifs ( H₂O, O₃, composite CO₂ + autres gaz bien mélangés ) en fonction de la longueur d'onde incidente sont très complexes. Et, pour un constituant donné, à une échelle très fine, une multitude de raies d'absorption peuvent coexister dans un très petit intervalle spectral ( on parle alors de bande d'absorption ).
On construit un modèle simple de bandes d'absorption en émettant des hypothèses sur la distribution des raies et leur intensité :
- la position des raies à l'intérieur d'une bande est supposée entièrement due au hasard, de sorte que la transmission résultant de toutes les raies d'un intervalle est égale au produit des transmissions de chaque raie de la bande.
- la forme de la distribution de probabilité de l'intensité d'une raie est calculée par le modèle de bande de Malkmus. On obtient ainsi pour chacun des intervalles spectraux, une largeur équivalente ( qui permet d'écrire la transmission simplement ) et ceci pour chacun des 3 gaz actifs. Puis on intègre sur tout le spectre à l'aide des approximants de Pade ( absorption moléculaire ) et des fonctions de e-type ( effets thermiques de l'eau ).

Par contre, dans le cas des corps gris ( aérosols, nuages et diffusion Rayleigh ) la formulation est simple et linéaire par rapport à la quantité de matière traversée.

5.4.1.4 intégration optique

Il faut tenir compte des chemins optiques parcourus par les différents photons se trouvant dans la couche considérée.

L'approximation de base est que l'on ne considère qu'un seul intervalle spectral pour chaque type de rayonnement ( solaire et infra-rouge thermique ).

Cas solaire :
Dans l'interaction entre diffusion multiple et absorption gazeuse, seuls l'absorption du rayonnement parallèle descendant et du rayonnement diffus réfléchi au sol sont calculés exactement, les autres termes étant approchés à travers des épaisseurs optiques gazeuses calculées dans les deux cas exacts et réutilisées telles quelles ensuite : On calcule les épaisseurs optiques en partant du sommet vers le sol ( évaluation du flux parallèle descendant ). On poursuit le calcul en repartant du sol vers le sommet, en se basant sur toute l'épaisseur optique de l'atmosphère qui vient d'être calculée. Ceci revient à considérer des rayons solaires réfléchis sur le sol et repartant vers l'espace.
Ces épaisseurs optiques servent à évaluer les flux diffus.

Cas thermique :
On suppose d'abord, de façon cohérente avec le reste du modèle dynamique, que l'atmosphère est un empilement de couches isothermes et qu'il y a discontinuité entre les couches.
Il y a trois sortes de termes à considérer :
1- le terme de refroidissement vers l'espace ( "cooling to space ) qui correspond au refroidissement du système terre/atmosphère par rayonnement vers l'espace. C'est un terme formellement équivalent au rayonnement solaire arrivant ( les photons repartent dans l'espace ).
2- les termes d'échange avec le sol
3- les termes d'échange avec les autres couches.
Le terme de refroidissement vers l'espace est prépondérant, il est calculé de façon exacte. Au vu des ordres de grandeur respectifs de ces termes, on peut se contenter d'une moins grande précision pour les termes d'échange.

Remarques :

Le coût du calcul croît seulement linéairement avec le nombre de niveaux du modèle ( ceci est vrai pour toute la physique ARPEGE, et pas par hasard ! ).

PAGE PRECEDENTE	PAGE SUIVANTE