| LINK TO NEW ALADIN WEB |
 |
| ALADIN Consortium |
| ALADIN Documents |
| ALADIN Model |
Next: About this document ... Up: Main page Previous: 5. Incremental form for
Subsections
6. Code aspects for ECMWF's LFULLIMP incremental form of the PC scheme
This section describes the code of the LFULLIMP option in the CY25 version.
6.1 General principles
- All grid point computations are perform with "non-incremental" (or full) variables X, the existence of "incremental" variables Y is totally limited to the spectral space. This requires the additional saving of the "background" variable in SP space in order to be able to compute the "increment" from the full variable and the "background" variable. The increase of memory of the incremental method come from this necessary eadditional storage.
- During GP part of predictor step, the prognostic variables labelled "PxT9" refers to time-level "-" (however they are not used), and the prognostic variables labelled" PxT0" refers to time-level "0" (to be documented more carefully).
- During GP part of corrector step, the prognostic variables labelled "PxT9" refers to time-level "0", and the prognostic variables labelled "PxT0" refers to time-level "*" (to be documented more carefully).
6.2 Data flow for incremental form
SUBROUTINE LATTEX :
- PxNLT9 : is used for storage of old values for next iteration in PC (or next time-step in SI)
- - Predictor step : Contains
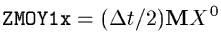
- - Corrector step : not used (because the next time-step is 2TL non-extrapolating)
- PxL9 : is used for High-Order interpolations at origin point
- - Predictor step : Contains
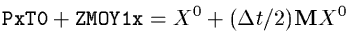
- - Corrector step : Contains
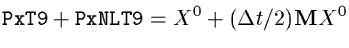
- (because PxT9 contains X0 in the corrector step,
- and PxNLT9 contains
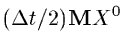 in the corrector step)
in the corrector step)
- PxT1 : is used for not interpolated quantities (at final point)
- - Predictor step : Contains
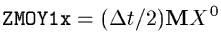
- - Predictor step : Contains
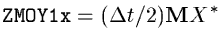
- (because ZMOY1x
contains
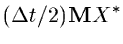 in the corrector step)
in the corrector step)
- PxL0 : is used for Low-Order interpolated
at origin point
- - Not used in PC scheme (no Low-order interpolations)
- PxSI : for Linear terms
- - Not used in PC scheme and more generally in incremental form.
Hence,
at the end of LATTEX, we have ![]() in PxL9 and
in PxL9 and ![]() in PxT1. We are thus ready to compute the RHS of (
3) and (6
) equations, except for the XF term in the first
RHS parenthesis of these equations.
in PxT1. We are thus ready to compute the RHS of (
3) and (6
) equations, except for the XF term in the first
RHS parenthesis of these equations.
SUBROUTINE LAPINEB :
In this subroutine, the RHS quantities
of (3) and (
6) computed at the final point and interpolated at the origin point
are aggregated. Hence, they almost form the RHS of the linear equation inversion
in its final form for the incremental variables Y* and
Y+ (as seen above, the
XF term is missing).
Following the definition in the introduction, we use the notation tilde for
the RHS of a linear inversion equation. Hence, after the
LAPINEB aggregation we have
![$[\widetilde{Y^*} + X^0_F]$](img55.gif) for the predictor-step, and
for the predictor-step, and ![$[\widetilde{Y^+} + X^*_F]$](img56.gif) for the corrector-step.
for the corrector-step.
Direct Spectral Transform
The method adopted to implement the incremental
form is to transmit from GP to SP space only the agregated RHS
![$[\widetilde{Y^+} + X^*_F]$](img56.gif) of the linear model inversion equations. The "background" variables are
needed in the spectral space to compute incremental variables from the full
variables and vice-versa. The "background" variables are thus saved in the
spectral space from one step or sub-step to the next one. With this method,
no additional transforms are thus needed.
of the linear model inversion equations. The "background" variables are
needed in the spectral space to compute incremental variables from the full
variables and vice-versa. The "background" variables are thus saved in the
spectral space from one step or sub-step to the next one. With this method,
no additional transforms are thus needed.
SUBROUTINE SPCSIX :
At the begining of spectral-space computations, we compute the definitive form of the linear inversion equation RHS from the provisional form and the "background" variable which has been saved at the previous step or sub-step (see below):
![\begin{eqnarray*}\widetilde{Y^*} & = & [\widetilde{Y^*}+ X^0_F] - X^0 \\
\widetilde{Y^+} & = & [\widetilde{Y^+}+ X^*_F] - X^*
\end{eqnarray*}](img57.gif)
Then the linear equation is inversed, giving the new variables in incremental form:
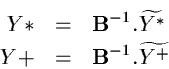
Then the full variables are restored from the background variables:
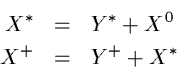
The new full variables are stored for the next step or sub-step:
End of predictor step: X* is saved for next sub-step.
End of corrector step: X+ is saved for next step.
These new full variables are spectrally-transformed back to the G.P space for next step or sub-step. The variable X * becomes X0 in G.P space for the corrector step GP computations, and the variable X+ becomes X 0 in G.P space for the next time-step GP computations.
6.3 Some details on Decentering
Provision is made in the code for more
flexibility on the amount of decentering ![]() between the various terms to which it is applied.
between the various terms to which it is applied.
In SUDYN : three values are defined:
- -
-
BCOR_HORIZ : which corresponds to
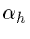 in the formalism of Cullen QJ paper, or to
in the formalism of Cullen QJ paper, or to
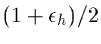 in the formalism of this note.
in the formalism of this note. - -
-
BCOR_VERT : which corresponds to
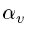 in the formalism of Cullen QJ paper, or to
in the formalism of Cullen QJ paper, or to
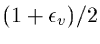 in the formalism of this note.
in the formalism of this note. - -
-
BCOR = MAX(BCOR_HORIZ , BCOR_VERT) which will be noted
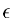 in this section
in this section
In LATTEX, (computation of
explicit model RHS) both ![]() and
and ![]() are used:
are used:
- -
-
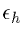 is applied to U and V equations
is applied to U and V equations - -
-
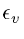 is applied to T and
is applied to T and 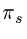 equations
equations - -
- the other variables are not decentered (q, qi, q l, O3, ...)
In LAVENT
, (trajectory research) only ![]() is used, but is applied only to the vertical component of the wind.
is used, but is applied only to the vertical component of the wind.
For the predictor step we thus have:
![\begin{displaymath}{\bf OF} = \frac{\Delta t}{2} \left[V^0_F + V^0_O + (1+\epsilon_v) w^0_F + (1-\epsilon_v)w^0_O \right]
\end{displaymath}](img70.gif)
And for the corrector step we have:
![\begin{displaymath}{\bf O^*F} = \frac{\Delta t}{2} \left[V^*_F + V^0_{O^*} + (1+\epsilon_v) w^*_F + (1-\epsilon_v)w^0_{O^*} \right]
\end{displaymath}](img71.gif)
where V is the horizontal wind vector, and w the vertical wind vector.
In SPCSIX
, (inversion of linear model) only ![]() is used.
is used.
Next: About this document ... Up: Main page Previous: 5. Incremental form for Pierre BENARD
2002-06-17
 |
Home |