The semi-Lagrangian (SL) semi-implicit (SI) method proposed by Robert (1981) has been investigated by many authors. The early versions of the method were three-time-level schemes since they were built on the basis of the previously existing Eulerian "Leap frog" schemes. Later on, the first two-time-level (2TL) schemes have proved to be more efficient and have been implemented into several operational models. One of the most important features of the early 2TLSL schemes was the extrapolation in time of the wind velocity to obtain the position of the middle point of the semi-Lagrangian trajectory. Temperton and Staniforth (1987) applied a linear extrapolation in time. We call this technique Classical 2TLSL.
Some discussions on the Classical 2TLSL can be found in Staniforth and Cote (1991). Already at that time, the extrapolation technique was recognized as a potential source of instability. However, no problems were reported at the time and the scheme was adopted worldwide. In some recent cases, characterized generally by strong wind gradients, spurious oscillations have been obtained with a number of 2TLSL models.
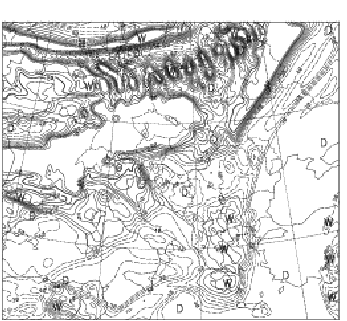
A typical example is the famous "Baltic Jet" case, where some non-meteorological
noise was observed in the core of a strong mid-troposphere jet and was
reported from almost all European 2TLSL models integrated over the East
Atlantic region. In Fig. 1 the instability can be seen in the relative
humidity field as a wave extended over the Baltic sea region.
The extrapolation in time for obtaining the middle point of the SL trajectory was identified as a source of the instability. Hortal (1998) studied the problem, developed and examined a new scheme which avoided the extrapolation and involved in the displacement computation only quantities from exact time steps. Hortal's scheme seemed to be successful in solving the noise problems and was adopted in all models linked to ECMWF/IFS.
Other problems of the SL technique are related to its interaction with orography. Similar oscillations to those in the "Baltic Jet" case can often be observed in the vicinity of mountains. The treatment of the non-linear residual of the forcing term in the momentum equation has been considered as a main source of such oscillations. The technique of spatial averaging was proved to reduce such noise and was adopted. As a result, the version of the Classical scheme for the non-linear residual, examined in this work, was invented. It consists of a linear extrapolation in time of the non-linear term and its averaging along the SL trajectory. Recently, Hortal (1998) contributed to solve the problem by implementing his SETTLS scheme also for the treatment of the non-linear residual.
In the first part of the thesis we make an attempt to analyze the 2TLSL method and examine the properties of different 2TLSL schemes. The instability problems, related to the 2TLSL trajectory scheme as in the "Baltic Jet" case, as well as the response of the SL to orography, related to the scheme for the treatment of the non-linear residual, motivated us to search for different solutions than the already existing ones. The insufficient conservation ability of the SL schemes has always been addressed as a disadvantage of the method. Several studies have measured how well certain quantities are conserved. To reveal the possible relationship between the choice of trajectory scheme and scheme for the non-linear residual, from one side, and the conservation of the model invariants in case of "Shallow Water" model, from the other side, is another objective.
In the beginning some general considerations are given. Then, an attempt to study the 2TLSL method analytically is presented. First, an exact solution of the 1D forced advection equation is introduced in order to illustrate the idea to use the explicit forcing term into the trajectory computation of the 2TLSL. Then, the second order accuracy of 2TLSL schemes is analyzed. As a result two theorems are derived and a particular trajectory scheme is proposed. The statements of the two theorems and the properties of various 2TLSL schemes are first examined with a simplified model which is designed to follow the computations of a 3D spectral NWP model.
The basic result from the analytical study and the experiments with the simplified model is that the uniform acceleration trajectory scheme is a very good solution for the trajectory problem of the 2TLSL method. In hydrostatic systems, the vertical momentum equation is reduced to a diagnostic balance equation between the pressure gradient force and the Earth attraction. The vertical velocity looses its independence as a prognostic variable. It is derived diagnostically from the continuity equation and has different level of complexity depending on the particular choice of vertical coordinate (see Kasahara 1974).
The problem with the explicit definition of the vertical momentum equation has never been put in consideration before because the 3TL schemes require a special treatment of the explicit terms coming from the numerical methods theory and providing stability while satisfying second order accuracy. The advection terms in the Eulerian model, for example, are treated in the same way for both the vertical and the horizontal. They are evaluated at the intermediate time level. In the 3TLSL scheme the vertical SL trajectory is computed in the same way as the horizontal one. The vertical velocity is evaluated at the intermediate time level and the middle point of the SL trajectory. An illustrative discussion on the 3TLSL and 2TLSL methods can be found in Staniforth and Cote (1991). The need of a redefinition of the discretization scheme for the vertical momentum equation in case of a hydrostatic model arises only in the 2TLSL.
In the first part of the thesis as well as in Gospodinov et al. (2001) it was demonstrated that an explicit estimate of the acceleration is required for a correct formulation of the trajectory scheme in case of a forced self advection one-dimensional problem. The proposed trajectory scheme has been named uniform acceleration trajectory scheme. Hortal (1998) also considered the possibility to apply the forcing term from the right-hand-side (RHS) of the horizontal momentum equation as an acceleration for the trajectory computation. However, he abandoned this approach in order to remain consistent with his vertical trajectory scheme.
The goal of the second part of the thesis is to examine the application of the uniform acceleration trajectory scheme also for the vertical 2TLSL trajectory in a hydrostatic model. For this purpose we derive an explicit estimate for the vertical acceleration in the environment of the hybrid vertical coordinate of Simmons and Burridge (1981). The particular choice is due to the choice of testing atmospheric model. It is the ALADIN model. Its dynamics is described first. Then the proposed vertical acceleration is presented built on the basis of the continuity equation. Then a comparison study of the same four trajectory schemes as in Gospodinov et al. (2001) but applied to the vertical 2TLSL trajectory in ALADIN. The schemes are tested for two different cases the "Baltic Jet" case dominated by horizontal advection and the "Cleopatra" case with a dominant vertical motion in a squall-line (see Banciu et al. 1999).
The perspectives in front of the 2TLSL method may be grouped in two parts. The first area of interest is in the hydrostatic atmospheric models. Since the global models with lower resolution will remain hydrostatic, it is important to keep the effort to improve the 2TLSL scheme for them. In this sense, the application of the proposed vertical trajectory scheme for a 2TLSL hydrostatic model can be beneficial. However, in the environment of a spectral model it requires significant additional computational effort mainly because of the second order derivatives necessary for the computation of the vertical acceleration. The examined vertical acceleration has also the disadvantage to be not complete in the diabatic case because of the incomplete tendency equation for the divergence. In a spectral model it is difficult to obtain derivatives of the physical tendencies. However, in case of a finite difference 2TLSL model, the explicit prognostic equation for the divergence could easily be completed in the diabatic case and the second order derivatives might require only small additional computational effort. In this case, the explicit trajectory scheme may be more efficient.
The second area of interest is the non-hydrostatic modeling. In this case, the implementation of the uniform acceleration trajectory scheme on the vertical is in general easier because the vertical velocity is an independent variable and has its own prognostic equation. However, the non-hydrostatic version of ALADIN is a particular one (see Bubnova et al. 1995). Its vertical coordinate system is kept identical to the one of the hydrostatic version of the model. The diagnostic vertical velocity is still active and used for the vertical SL trajectory computation. Hence, the proposed vertical acceleration can be beneficial for the non-hydrostatic model as well.
References:
Banciu, D., Gerard, L., and Geleyn, J.-F., 1999: `High resolution study of a squall line'. pp. 158--168 in LAM Newsletter, n. 28, Danish Meteorological Institute, Copenhagen, Denmark
Bubnova, R., Hello, G., Benard, P., and Geleyn, J.-F., 1995: Integration of the fully elastic equations cast in the hydrostatic pressure terrain-following coordinate in the framework of the ARPEGE/Aladin NWP system. Mon. Weather Rev., 123, 515-535
Gospodinov, I. G., Spiridonov, V. G., and Geleyn, J.-F., 2000: Second order accuracy of two-time-level semi-Lagrangian schemes. Q. J. R. Meteorol. Soc., 127, 17pp.,(accepted)
Hortal, M., 1998: `New two-time-level semi-Lagrangian scheme'. ECMWF memorandum research dept., 18pp. (Available from ECMWF, Shinfield Park, Reading RG2 9AX, UK)
Robert, A., 1981: A stable numerical integration scheme for the primitive meteorological equations. Atmos.-Ocean, 19, 35-46
Simmons, A., J. and Burridge, D., M., 1981: An energy and angular-momentum conserving vertical finite-difference scheme and hybrid vertical coordinate. Mon. Weather Rev., 109, 758-766
Staniforth, A. and Cote, J., 1991: Semi-Lagrangian integration schemes for atmospheric models - review. Mon. Weather Rev., 119, 2206-2223
Temperton, C. and Staniforth, A., 1987: An efficient two-time-level semi-Lagrangian semi-implicit integration scheme. Q. J. R. Meteorol. Soc., 113, 1025-1039